30 év múlva: kiemelkedő eredmény a számítástudományban

Az elmúlt hetekben szárnyra kapott a hír a számításelmélet iránt érdeklődők körében: Babai László professzor áttörést jelentő eredményt ért el egy nevezetes számítási feladattal, a gráfizomorfizmus-problémával (röviden GI) kapcsolatban.

Mi is ez a feladat, és mi teszi kiemelten fontossá? A feladat bemenete két véges hálózat, G és H, mindkettő csomópontokból és köztük levő kapcsolatokból, szokásosabb nevükön élekből áll. El kell dönteni, hogy a két hálózat izomorf-e. Az izomorfia azt jelenti, hogy G csomópontjait kölcsönösen egyértelműen megfeleltethetjük H csomópontjainak úgy, hogy ez a megfeleltetés megtartja a kapcsolatokat és azok hiányát is. Ha két G-beli csomópont között van kapcsolat (él), akkor a nekik megfelelő H-beli pontpár között is van. Ha pedig a két G-beli csomópont között nincs él, akkor a H-beli megfelelőik között sincs.

A következő ábrán három hálózat látható, mindegyiknek négy csomópontja van. Az első kettő izomorf egymással, egy lehetséges megfeleltetés 1 ↔ a, 2 ↔ b, 3 ↔ c, 4 ↔ d. Az első és a harmadik hálózat viszont nem izomorf egymással: az elsőnek négy éle van, a harmadiknak pedig öt.

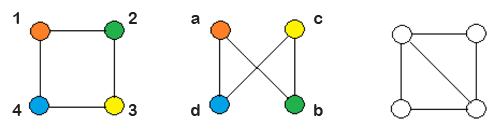
Ezzel egyenértékű kérdés a struktúrák szimmetriáinak felismerése, ami ugyancsak több matematikai terület központi kérdése.

A gyakorlatban is felbukkan a GI-feladat kémiai hálózatok (ahol a csomópontok atomok, a kapcsolatok kémiai kötések) és elektronikus áramkörök (a csomópontok áramköri elemek, a kapcsolatok összeköttetések) elemzése során.

Ki kell emelnünk, hogy Babai László új algoritmusa (ha helyessége bebizonyosodik) elméleti téren jelent áttörést; a gyakorlatban felmerülő gráfokra régóta ismeretesek hatékony programok (Brendan McKay és Adolfo Piperno módszerei). Ezeknél azonban nincs elméleti garancia arra, hogy minden esetben hatékonyan működnek. Az ilyen elméleti garanciák keresése a számítástudomány központi törekvése.

Babai László
Forrás: www.snipview.com

A GI-feladat különleges helyet foglal el a számításelméletben.

Az NP feladatosztályba az olyan eldöntendő (igen-nem választ váró) számítási feladatok tartoznak, amelyeknél az igen válasznak van hatékonyan ellenőrizhető tanúja. A tanú olyan információ, amelynek birtokában gyorsan ellenőrizhető az igaz válasz helyessége. Például annak a ténynek, hogy az ábrán az első két hálózat izomorf, az 1 ↔ a, 2 ↔ b, 3 ↔ c, 4 ↔ d megfeleltetés ilyen értelemben hatékonyan ellenőrizhető tanúja.

Az NP feladatosztály rendkívül gazdag, szinte minden alkalmazási területről találhatunk itt feladatokat. Az elméleti értelemben hatékony algoritmussal megoldható igen-nem feladatok alkotják benne a P részosztályt: a polinom időben megoldható feladatok osztályát. Ezek a könnyűnek, jól kezelhetőnek mondható feladatok az NP-n belül.

Idetartoznak az egyszerűbb útkeresési problémák. Például az a kérdés, hogy egy hálózat adott M és J csomópontja között van-e a hálózat éleit követő olyan út, amelyik megadott számú, vagy annál kevesebb élt használ. Az NP osztály felső részébe képzelhetjük el az NP-teljesnek nevezett feladatokat. Ezek az osztály legnehezebbjei. A pakolási feladatok között különösen gyakran találkozhatunk velük.

Nehézségüket érezhetjük, amikor nagyméretű kirakós játékkal kell megbirkóznunk. Az NP-teljes feladatokra nem ismert hatékony megoldó módszer. Sőt, a híres P/NP sejtés szerint ilyen módszer nemcsak a jelenlegi tudásunk korlátai miatt nem ismeretes, hanem egyáltalán nem is lehetséges.

Ez a sejtés a jelenkori matematika egyik legfontosabb megoldatlan kérdése.

A sejtés kimondja, hogy az NP feladatosztály bővebb a P osztálynál.

Az NP osztálynak ezt az egyszerű tagozódását szemlélteti az alábbi ábra:

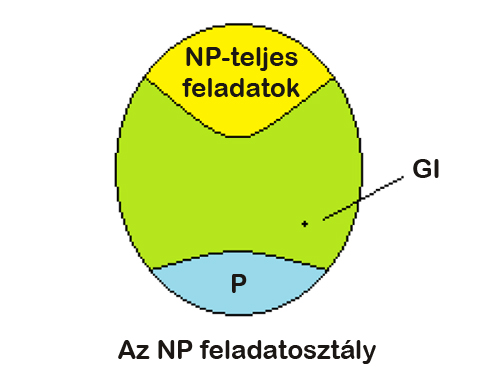
A szakértők nagy többsége azt gondolja, hogy a két osztály különböző: az NP nagyobb a P-nél. A két feladatosztály egyenlősége azt jelentené, hogy minden NP-beli feladatra van hatékony algoritmus. Ismert továbbá, hogy ha tényleg nagyobb az NP, mint a P, akkor vannak az NP-ben köztes nehézségű feladatok is: olyanok, amelyek nincsenek P-ben, de nem is NP-teljesek.

Különös tapasztalati tény ugyanakkor, hogy míg se szeri, se száma a P-beli és az NP-teljes feladatoknak, addig viszonylag kevés természetes feladatot ismerünk, ami köztes nehézségű lehet. Másképp fogalmazva: egy új NP-beli kérdésről rendszerint hamar kiderül, hogy vagy P-beli, vagy pedig NP-teljes.

Itt térhetünk vissza a GI-problémához. Ez egyike azon kevés, központi jelentőségű számítási feladatoknak, amelyek a mai tudásunk szerint a közbülső részben vannak. Nem ismert, hogy NP-teljes lenne, de az sem, hogy P-be tartozna, vagyis létezne hatékony algoritmus a megoldására.

Az izomorfizmusfeladat sokféle speciális hálózatra hatékonyan megoldható, például azokra, amelyekben a csomópontoknak csak kevés (mondjuk, maximum 6) szomszédjuk lehet. Tetszőleges hálózatokra működő hatékony algoritmus azonban nem ismert. A legjobb időkorláttal rendelkező algoritmusok erre a feladatra - és néhány közeli rokon problémára - az 1980-as évek elején születtek, E. M. Luks, Babai László és V. N. Zemljacsenko munkája nyomán. Ezekben az időkorlát mérsékelten exponenciális (exponenciális a csúcsszám négyzetgyökének a függvényében), ami igen komoly javítást jelent a legegyszerűbb eljárásokhoz képest, ám nagyon távol van a hatékony algoritmusoktól elvárt (ún. polinomiális) növekedési rendtől.

A GI elméleti jelentőségét azzal is érzékeltethetjük, hogy külön könyv is foglalkozik vele.

A Chicagói Egyetem két tanszéke (matematika, számítástudományi) jelentette be a honlapján, hogy Babai professzor három előadásban (november 10., 12., 24.) számol be új eredményéről, miszerint a korábbinál sokkal kedvezőbb (ún. kvázipolinomiális) időkorláttal rendelkező algoritmust talált a gráfizomorfizmus-feladatra.

A bejelentést nagy érdeklődéssel és izgalommal teli várakozással fogadta a szakma. Például Scott Aaronson, a világ vezető műszaki egyeteme, az MIT professzora sokak által követett tudós blogjában kiemelte, hogy a számítástudomány egyik központi jelentőségű algoritmikus feladata került közel a P osztályhoz. ,,Ez lehet az évtized számításelméleti eredménye" – írja Aaronson.

A bejelentésről több tudományos magazin is beszámolt: a Science, a Science News, a New Scientist, valamint a Nature.

Babai László első szemináriumi előadásán a szokásos 15-30 fő helyett mintegy 200-an jelentek meg. Az egyik jelenlévő élő tweet-adásban közvetítette a hallottakat, amelynek alapján olyan tudományos kiválóságok, mint a Fields-érmes Timothy Gowers és Terence Tao bocsátkoztak nyilvánosan találgatásokba Babai megoldásának természetéről.

Az előadás videofelvétele itt látható.

A Knuth-díj laudációja hangsúlyozza, hogy Babai ,,fogalmi újításai és úttörő munkássága (...) átalakította a számításelmélet tájképét". A laudáció kiemeli Babai úttörő szerepét a matematikai bizonyítás több évezredes fogalmának újraértelmezésében, ami ,,a közel optimális megoldások nehézségének elméletében alapvető felismerésekre vezetett". A méltatók azt is megemlítik, hogy ,,Babai meghatározó vezető egyénisége volt az algoritmikus csoportelmélet megalkotásának és a gráfizomorfizmus-probléma kutatásának; utóbbi az egyik legfontosabb olyan probléma, amelynek a bonyolultsága még tisztázatlan. Úttörő jelentőségű korai munkáiban alapvetően új, csoportelméleti megközelítést vezetett be, amely motiválta a feladat megoldására szolgáló legjobb ismert algoritmusok kifejlesztését..."

Sportnyelven szólva tehát Babai professzor az egyike azoknak, akik a régi rekordot elérték, és most – három évtizeddel később – neki sikerült ezt egészen döbbenetes mértékben megjavítania.

Rónyai Lajos

Ahogy honlapján ő maga is figyelmeztet: gondolatmenetének helyességét még nem ellenőrizték más szakértők. Erre még várni kell, de reméljük, hamarosan erre is sor kerül, és akkor egy világraszóló új eredménynek örülhetünk.

Rónyai Lajos