A csábító korlátos dimenziók – Pach János ERC Advanced Grant-nyertes

Ha megkérdezünk valakit, hogy mire emlékszik iskolai geometriatanulmányaiból, nagyjából borítékolható a reakció: hosszú kínos csend, majd tétován elővánszorgó szófoszlányok: szögösszeg..., háromszög…, köré… belsejébe… írt kör..., Pithagorasz…, talán Thalész… „Időm értékes” – mondja némi gúnnyal az átlagkamasz az ősi görög tudásra, és az érettségi rendszerint egy kiterjedés nélküli, de igen határozott pontot tesz a geometriával ápolt kényszerű kapcsolatának végére.

Van azonban a geometriának egy másik, játékosabb arca is. A témakör kezdetei a XIX. század végéig nyúlnak vissza, James Sylvester angol matematikus észrevételeihez, de igazán a XX. század közepén indult fejlődésnek, jórészt a világhírű magyar matematikus, Erdős Pál néhány látszólag ártatlan problémájának köszönhetően. Erdős, akit Issai Schur, berlini professzor már a 30-as években a „budapesti mágusnak” nevezett el, híres volt arról, hogy képes volt bűvészcilinderéből olyan egyszerűen megfogalmazható kérdéseket előhúzni, melyek mély matematikai problémákra világítottak rá, és melyekkel matematikusok generációi birkóztak-birkóznak több-kevesebb sikerrel. Ezt az újfajta, „játékos” geometriát Pach János Erdős egy klasszikus kérdésével illusztrálta.

Erdős Pál (balra) és a budapesti matematikai kutatóintézet alapítója, Rényi Alfréd Forrás: networksciencebook.com

Képzeljük el, hogy van n pontunk és ugyanennyi egyenesünk. Teljes szabadságunk van abban, hogy a síkon hova helyezzük el a pontokat, és milyen irányban fektetjük le az egyeneseket – csak annyi a kikötés, hogy különböző helyre tegyük őket, vagyis pont ponttal, egyenes egyenessel nem eshet egybe. A kérdés: összesen legfeljebb hányszor fordulhat elő, hogy pont illeszkedik egyenesre? (Ha pl. két pont van egy egyenesen, vagy két egyenes megy át egy ponton, azt két illeszkedésnek vesszük.)

Szólítson csak nagy N-nek!

Ez a feladat valószínűleg Eukleidésznek is tetszett volna, hiszen csak pontok, egyenesek és illeszkedések, az euklideszi geometria alapfogalmai szerepelnek benne. Megoldása mégis teljesen más jellegű gondolkodást igényel, mint a geometria atyja által több mint kétezer éve felvetett kérdések túlnyomó többsége. Az egyik legszembetűnőbb különbség, hogy a kérdésben fontos szerepet játszik n, a pontok és az egyenesek száma. Ahány n, annyi külön feladat. Papíron rajzolgatva, ha van kedvünk, érdemes eljátszanunk 1, 2, 3, 4, esetleg több ponttal. Az illeszkedések számában (3n-3)-at nagyon egyszerű elérni. (Vegyünk fel például n-1 pontot egy egyenesen, az n-iket pedig tegyük valahova az egyenesen kívül, és kössük össze az egyenesen levő mindegyik ponttal.) Ezzel szemben n² illeszkedés – vagyis amikor minden pont minden egyenesre illeszkedik és viszont – már akkor sem lehet, ha n=2, hát még ha nagyobb.

A kérdés: hol az igazság a kettő között? Van-e valamiféle „trend”, szabályosság, vagy minden n-re egy teljesen más feladatot kapunk teljesen más megoldással? A válaszra 40 évet kellett várni. 1983-ban Szemerédi Endre és Tom Trotter bebizonyították, hogy – amint azt Erdős sejtette – az illeszkedések maximális száma nagy n esetén körülbelül n^4/3. Ez a korlát valószínűleg csak akkor érhető el, ha pontokat „rácsszerűen” helyezzük el, de ezt – amint Pach János mondja – senkinek sem sikerült igazolnia. Eleinte az ehhez hasonló feladatokban sokan nem láttak többet izgalmas agytornánál. Nem volt igazuk.

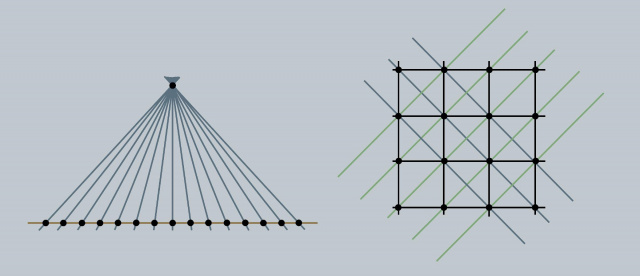Az ábrán az n=16 eset két lehetséges megvalósítása látható. A bal oldalon, a vízszintes egyenesen 15 pont van, a másik 15-ön 2-2. Ez osszesen 15+15·2 = 45 érintkezés. Jobbra a rácsszerű elrendezés előnyei, szintén n=16 esetén. Látható, hogy az egyszerű négyzetrács vonalai mellett a rács geometriájából adódó különféle átlók is segítik az érintkezések számának növelését. A kérdés csak az, hogy milyen gyorsan bővülnek ezek a lehetőségek, ahogy n nő? Itt összesen 56 illeszkedést találunk. Forrás: mta.hu

Szemerédi és Trotter tétele fontos számelméleti és algebrai problémákhoz kapcsolódik. A 80-as években az is kiderült, hogy központi szerepet játszik a geometriai algoritmusok elméletében is. Miért vált hirtelen érdekessé, hogy mi egy feladat megoldása, ha n rendkívül nagy? Időközben ugyanis ránk virradt a nagy n-ek kora, nem kis mértékben egy magyar nagy N-nek, Neumann Jánosnak köszönhetően. A digitális számítógépek egyre növekvő kapacitása olyan problémák megoldását tette lehetővé, melyekről korábban álmodni se mertek. Bebizonyosodott, hogy a számítógép sebességéből adódó „nyers erő” megsokszorozható kombinatorikai tételekre támaszkodó hatékony algoritmusok segítségével.

A nagy n „átka” a geometriai jellegű alkalmazásokat sem kímélte, hiszen ami a való világban egyszerű geometriai alakzat, az a számítógép képernyőjén sok millió képpont halmaza. Ha körbenézünk egy virtuális világban, a számítógépnek e virtuális világ minden egyes objektumáról el kell döntenie, hogy melyik látszik a mi nézőpontunkból és melyik nem. Gondoljunk csak bele, hogy mindez milyen bonyodalmakhoz vezet, ha a képernyő felbontása és a virtuális világ objektumainak száma növekedni kezd. Márpedig nem kérdés, hogy kezd: hasonlítsunk össze egy tíz éve készült számítógépes játékot egy maival.

A programozóknak, grafikusoknak egyáltalán nem mindegy, hogy egy probléma mennyivel válik bonyolultabbá, ahogy a képfelbontás, illetve az objektumok száma nő. Előfordulhat, hogy teljesen más megközelítésre kell áttérniük, ha mondjuk full HD-ről 4K-ra váltanak. Egy nyüzsgő piac jó megjelenítéséhez olyan grafikus kártyára lehet szükség, amilyen ma még nem is létezik. Az ilyen fejlesztésekben pedig fontos szerepet játszanak a matematikusok is.

Pach János

Számítógépes játékok, zongorák, robotok

Pach János szakmai pályafutását az MTA Matematikai Kutatóintézetében kezdte, melyet azóta az intézet alapítójáról, Rényi Alfrédról neveztek el. Az igazgató akkoriban Fejes Tóth László volt, akit a magyar diszkrét geometriai iskola úttörőjeként ismerhetünk. Pach Jánost – jóllehet szakdolgozatát véges és végtelen kombinatorikai problémákról írta, és saját elmondása szerint fogalma sem volt arról, hogy mi a diszkrét geometria – adminisztratív okoknál fogva Fejes Tóth diszkrét geometriai csoportjába osztották be. Az intézet hagyományaihoz híven azonban az igazgató biztosította arról, hogy olyan feladatokon gondolkozhat, amilyeneken csak akar.

Fejes Tóth László

„Elbűvöltek Fejes Tóth gyönyörű kérdései, melyek többsége gömbök és más geometriai alakzatok valamilyen szempontból optimális elhelyezéseire és fedéseire vonatkoztak. Észrevettem, hogy a feladatok egy része rokonságot mutat az Erdős-féle kombinatorikával” – mondta. Amikor Pach az 1980-as évek közepén a New York-i Egyetem Courant Intézetében, a számítógépes geometria és a robotika egyik fellegvárában kezdett dolgozni, kiderült, hogy az otthonról hozott kombinatorikai és geometriai módszerek nagyszerűen használhatóak az ezen a területen felmerülő algoritmikus és extremális problémák megoldására. „Óriási szerencsém volt! Olyan kiváló tudósok társaságában, mint Jack Schwartz, Micha Sharir és a Princetonból gyakran odalátogató Bernard Chazelle, aktív részese lehettem egy új tudományág megszületésének.”

Manapság, amikor a kritikusok a Macskák moziváltozatában a színészek digitális bundáján élcelődnek, vagy egyes számítógépes játékokban az a kérdés, hogy főszereplőnk egyenként ellőheti-e a fák leveleit, már eszünkbe se jut, hogy a „hőskorban” a programozóknak mennyi ügyes mérnöki és matematikai trükkre volt szükségük, hogy az akkoriban elérhető gépek bírják szuflával. Ennek egyik látványos megnyilvánulása, hogy a tárgyakat és az ellenfeleket sokszor vonalak vagy sík felületek határolták (olykor ügyes textúrával elfedve). Itt a programok csak a sík- és térbeli idomok csúcsainak, éleinek és lapjainak mozgását követik, azután valahogy kitöltik a hiányzó részleteket. Kiderült, hogy számos grafikus feladatnál a leggyorsabb algoritmusok futásideje lényegében arányos a mozgástérbe eső „leszögletesített” objektumok csúcsainak számával. Ezt a mérőszámot gyakran a feladat „kombinatorikus bonyolultságának” nevezik. A baltával faragott arcok (Alone in the Dark) és a vonalrajzok (Elite) jobbára eltűntek a monitorokról – a Minecraft egy különös kivétel –, de a kombinatorikus bonyolultság fogalma ma is kulcsszerepet játszik az algoritmikus és kombinatorikus geometriában.

Az 1992-ben kiadott Alone in the Dark az egyik első olyan számítógépes játék volt, melyben részletesen kivitelezett háttér előtt szabadon mozgathattunk háromdimenziós figurákat. Egy kis emlékeztető: akkoriban egy számítógép 4 megabájt (!) memóriával és 120 megabájtos (!!!) merevlemezzel komolynak számított.

Pach egy másik példája a következő. Képzeljük el, hogy a bútorüzletben állunk a vágyaink tárgyát képező kétajtós szekrény előtt, és azon morfondírozunk, hogy fel tudjuk-e vitetni a szűk lépcsőházban anélkül, hogy levernénk a vakolatot. A robotikában az efféle feladatokat – az ormótlan berendezési tárgyak koronázatlan királya után – „a zongoraszállító problémája” összefoglaló névvel illetik, úrrá lenni rajtuk pedig egyáltalán nem egyszerű. Ilyesfajta feladatok sorának gyors megoldására van szükség, ha például egy mentőrobotnak kell segítenünk, hogy merre tud áthaladni a törmelék labirintusán. Akárcsak az előbb említett grafikus feladatnál, a leghatékonyabb algoritmus futásideje itt is a környezet kombinatorikus bonyolultságától függ. Ha ez túl nagy, akkor a kombinatorikai módszerek nem segítenek, és teljesen másféle mérnöki praktikákra van szükség.

A kombinatorikus bonyolultság korlátozásának igénye mély kombinatorikai, geometriai, topológiai és algebrai problémák egész sorát vetette fel. A felmerült kérdések közül sokat sikerült megválaszolni – részben az Erdős-féle kombinatorikai módszerek segítségével. De jelentős részük valószínűleg még évtizedekig foglalkoztatja a matematikusokat és számítógéptudósokat, és további tudományos meglepetések sokaságával szolgál.

Korlátos bonyolultság, korlátos dimenziók

A kombinatorikus módszerek alkalmazásának megvannak a maga korlátai. Nem egyszer olyan optimalizálási feladatok merülnek fel, melyekről – viszonylag természetes feltevések mellett – bebizonyítható, hogy megoldásuk a leggyorsabb gépeken futtatott leghatékonyabb algoritmusok segítségével is évszázadokig tartana. Ezekben az esetekben lényegében nincs olyan módszer, amely sokkal jobb lenne annál, mint hogy minden esetet szisztematikusan végigpróbáljunk, és kiválasszuk közülük a legjobbat. Az esetek száma pedig a feladat méretével, dimenziójával exponenciálisan nő. Ezt a jelenséget nevezik a „dimenzió átkának”. Nincs mit tenni ellene.

Vagy mégis? A gyakorlati és matematikai alkalmazások jelentős részében a szóban forgó struktúrák elég speciálisak. Sokszor előfordul, hogy az ilyen speciális tulajdonságokkal rendelkező objektumok, „esetek” száma nem is exponenciálisan nő. Ez a megállapítás viszonylag természetesnek tűnik olyan geometriai feladatok esetén, melyeknél maguk a vizsgált objektumok egy korlátos dimenziós tér részhalmazai, vagy beágyazhatóak egy alacsony dimenziós térbe, melyben minden objektumot korlátosan sok (mondjuk d) változó ír le. Ilyenkor a szóba jövő struktúrák szerkezete gyakran jóval egyszerűbb, számuk is jóval kisebb, és a feladat kezelhető. Sok esetben nem ennyire egyértelmű, hogy mi a feladat dimenziója, de végül is létezik egy ilyen „rejtett” paraméter.

Pach János ERC Advanced Grant által támogatott projektjének egyik célkitűzése az, hogy a geometriai intuíció által inspirált módszereket alkalmazza olyan nehéz kombinatorikus feladatok vizsgálatára, melyek közül soknak első látásra nincs sok köze a geometriához. Három példát is említ: az első geometriai, a másik kettő egyéb területre vezet.

Mikrocsipek és közvélemény-kutatás

Az első problémát Turán Pál vetette fel még az 1940-es években. Vegyük egy elektromos hálózat kapcsolási rajzát, „gráfját”, tehát n pontot a síkban, melyek közül bizonyos pontpárokat egyenes szakasszal kötünk össze. Ha elég sok összeköttetés van, akkor a szakaszok között elkerülhetetlenül lesznek olyanok, amelyek metszik egymást. Mennyi a kereszteződések minimális száma a legjobb lerajzolásnál, vagyis ha a pontokat a lehető legjobb helyre tesszük? Ennek meghatározása nagyon nehéz feladat. Nincs, és valószínűleg nem is lehet rá gyors algoritmust adni anélkül, hogy az összes lehetséges elhelyezést kipróbálnánk.

Abban az esetben, ha a gráfnak elég sok éle van, Jacob Foxnak, Pach Jánosnak és Andrew Suknak sikerült ilyen algoritmust találnia a feladat közelítő (mondjuk 1%-osnál kisebb hibával való) megoldására. A siker titka, hogy a gráf minden éle leírható négy számmal, nevezetesen két végpontjának két-két koordinátájával. Azt, hogy két él metszi egymást, könnyen eldönthető az őket leíró pontnégyesek ismeretében néhány – mondjuk d darab – polinomiális (tehát különféle hatványok összegét tartalmazó) egyenlet vagy egyenlőtlenség segítségével. Ez a d szám, melyet a feladat „dimenziójának” neveznek, korlátos, vagyis nem függ n-től, a gráf pontjainak a számától. Külön érdekesség, hogy a megoldás szempontjából alig számít, hogy ez a korlát mekkora: 5, 10 vagy 100. Elsőre ezeket a kérdéseket is a szórakoztató matematikai rejtvények közé sorolhatnánk. Csakhogy az 1980-as évekre kiderült, hogy nagy jelentőséggel bírnak a mikrocsipgyártásban. A legkisebb integrált áramkör mérete, mellyel egy adott hálózat megvalósítható, éppen attól függ, hogy milyen kevés kereszteződéssel rajzolható a síkba.

Pach második példájának inkább a szociológiához és a statisztikához van köze. Tegyük fel, hogy egy közvélemény-kutató intézet valamilyen fontos kérdésről reprezentatív felmérést szeretne végezni. Természetes elvárás, hogy a megkérdezettek között legyen valaki a társadalom minden jelentős csoportjából. Mondjuk az a cél, hogy minden fontos, tízezer főnél nagyobb csoportból megkérdezzünk legalább egy embert. A kérdés: mekkora mintát vegyünk? Nos, ezer főre biztosan szükség lesz, hiszen Magyarország lakossága 10 millió fő körül van, és szeretnénk, ha a mintánkban minden földrajzilag behatárolható csoport megjelenne. De kell-e több? És ha igen, hányszor annyi? Hány ezer főt kell kiválasztanunk ahhoz, hogy legyenek közöttük férfiak, nők, szülők, egyedülállók, a különböző korcsoportok tagjai, a nagyobb futballcsapatok szurkolói, a politikai pártok támogatói, nemzetiségiek és így tovább? Lesznek olyan csoportok, amelyek nagyjából egybeesnek vagy tartalmazzák egymást, de olyanok is, melyek teljesen különbözőek. A csoportok, „halmazok” elképesztően bonyolult rendszere összességében valamilyen értelemben a társadalom felépítésének „gazdagságát” adja meg. Két szovjet statisztikus, Vlagyimir Vapnik és Alekszej Cservonenkisz az 1960-as évek végén rájött arra, hogy amennyiben ennek a halmazrendszernek a bonyolultsága, azaz valamilyen – jól meghatározott értelemben vett – „dimenziója” kicsi, akkor elég egy viszonylag kis véletlen mintát venni. Ezt – az eddig említetteknél absztraktabb – dimenziót azóta róluk nevezték el. A Vapnik–Cservonenkisz-dimenzió nemcsak a statisztika tudományát forradalmasította, de kiderült, hogy döntő szerepe van a mesterséges intelligenciában (például arcfelismerő algoritmusok tervezésénél) és a kombinatorikus geometriában is.

Vlagyimir Vapnik (balról a második) és Alekszej Cservonenkisz (balról a negyedik) egy 1998-as konferencián Forrás: cml.rhul.ac.uk

Pach harmadik példája a korábban már említett Issai Schur egy több mint 100 éves tételéhez kapcsolódik, amely a kombinatorika egyik leggyorsabban fejlődő ága, a Ramsey-elmélet egyik kiindulópontja volt.

Jelöljünk ki sok pontot egy papírlapon, és kössük össze bármely kettőt valamilyen színű éllel. Összesen csak n színt használhatunk, és tilos létrehoznunk egy olyan háromszöget, melynek minden éle ugyanolyan színű. Belátható, hogy ha legfeljebb 2ⁿ pontot vettünk fel, akkor még van ilyen színezés, de ha annál sokkal többet, akkor nincs. Legfeljebb hány pont esetén oldható meg ez a feladat? Erdős azt sejtette, hogy ha a pontok száma az exponenciálisnál gyorsabban nő, akkor már nem oldható meg. Ezt máig sem sikerült senkinek igazolnia vagy megcáfolnia. A nehézség itt is abban rejlik, hogy a színezések száma sokkal nagyobb, mint a pontoké. Azonban a feladatot úgy is meg lehet közelíteni, hogy csak olyan színezéseket nézünk, amelyeket le lehet írni valamilyen egyszerű algebrai szabállyal. E fogalom megfelelő tisztázásával el lehet jutni a színezések „dimenziójának” egy lehetséges definíciójához. Kiderült, hogy ha csak az ilyen értelemben korlátos dimenziójú színezésekkel foglalkozunk, akkor az Erdős–Schur-sejtés igaz. Pach János kutatási tervének egyik lényeges célkitűzése, hogy más fontos kombinatorikus sejtéseken is kipróbálja ezt a módszert, valahogy így:

• Először a vizsgálat tárgyát le kell szűkíteni korlátos bonyolultságú, korlátos dimenziójú objektumokra.
• Ha emellett a megszorítás mellett a probléma sikerrel megoldható, akkor tovább lehet lépni a teljes megoldása felé.
• Az is lehet, hogy a vizsgálatok során találnak egy korlátos dimenziójú ellenpéldát, és az eredeti sejtés módosításra szorul.

Az efféle megszorítások gyakran könnyebben kezelhetőek, mint az eredeti kérdés, hiszen megoldásukhoz a modern kombinatorika és gráfelmélet eszközei mellett be lehet vetni a geometria és a topológia teljes fegyvertárát.

A kutatásban Pach János kulcsszerepet szán két kollégájának, akikkel az elmúlt 30 évben több tucat közös tanulmányt írt. Az egyikük Tardos Gábor, az MTA levelező tagja, Lendület-ösztöndíjas kutató, a másikuk pedig Pach korábbi doktorandusza, Tóth Géza, a matematikai tudományok doktora. Mindketten a Rényi Intézet munkatársai. Rajtuk kívül részt vesz a kutatásban két további világhírű matematikus: Andrew Suk, a University of California professzora, aki szintén Pach János diákja volt New York-ban, valamint Jacob Fox stanfordi professzor, aki egyetemista kora óta dolgozik vele.