Hasonló hálózatok és a meglepően gyors növekedés matematikája – Pyber László ERC-ösztöndíjának nyomában

„Összefoglaló cikkünk a friss ERC Advanced Grant-nyertesekről itt olvasható.Apu a nagyszobában pályázatot ír” – ez volt Pyber László fiának első összefüggő mondata úgy nyolc évvel ezelőtt. A srác ma már iskolás, apja, az MTA Rényi Alfréd Matematikai Kutatóintézet munkatársa pedig negyedik próbálkozása nyomán végül idén elnyerte az ERC Advanced Grant támogatását. Így nagyjából kétmillió euróval kezdhet kidolgozni valamit, aminek körvonalai már most felsejlenek a matematika hatalmas térképén.

Ahhoz azonban, hogy megértsük, miről is van szó, nem árt, ha egy kicsit közelebbről megismerkedünk ezzel a térképpel vagy legalábbis egyes részeivel.

Pyber László Fotó: mta.hu/ Szigeti Tamás

I. A hálózatok lényegéről

Egy lagziban járunk. A vőfély megkéri az egybegyűlteket, hogy álljanak fel egy körbe, és akik ismerik egymást, feszítsenek ki egy-egy piros szalagot. Ezután a fotós felrepít egy drónt a társaság fölé, és készít egy képet. A násznép annyira jónak tartja a mókát, hogy másnap reggel búcsúzásképpen megismétlik a játékot – persze senki sem emlékszik már arra, hogy is álltak előző nap.

Ha megnézzük a két képet, a piros szalagok hálózata valószínűleg teljesen máshogy fest, a háttérben rejlő kapcsolatrendszer azonban ugyanaz. Most pedig képzeljük el, hogy kapunk két ilyen hálózatot (a matematikusok nyelvén gráfot), és el kell döntenünk, hogy a háttérben levő kapcsolatrendszer valóban megegyezik-e, vagyis át tudjuk-e rendezni a csúcspontokat úgy, hogy megkapjuk a másik hálózatot. Ez a gráfizomorfizmus-probléma, amely nemcsak hogy nehéz feladat, de úgy tűnik, hogy a résztvevők (csúcspontok) számának növekedésével rohamosan nehezebbé válik.

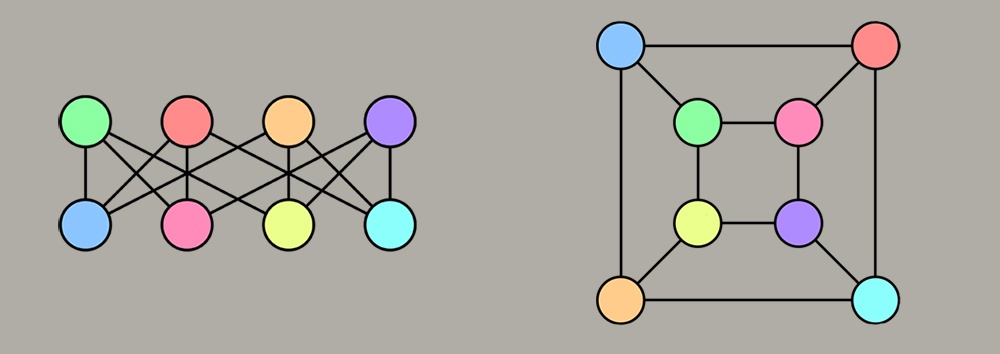Ez a két hálózat igencsak különbözőképpen néz ki, a lényegüket adó kapcsolatrendszer azonban ugyanaz – nézzük csak meg, melyik színek szomszédosak! A hálózati ábrák forrása: Wikimedia Commons/Booyabazooka – CC-BY-SA

Kissé furcsának tűnhet, de az előző mondatból a matematikusok számára a „rohamosan nehezebbé válik” kitétel a megfoghatóbb. Azt érdemes ugyanis vizsgálni, hogy ha a feladat méretét (esetünkben a násznép létszámát) növeljük, mennyivel több lépésre van szüksége a lehető legügyesebb algoritmusnak a feladat megoldásához. Eszerint vannak „egyszerűen kezelhető” (szaknyelven polinomiális vagy P-beli) problémák, melyeknél a lépések száma a probléma méretével viszonylag lassan nő, és „rohamosan nehezebbé váló” problémák, ahol a lépések száma a méret növekedtével egy idő után kezelhetetlen gyorsasággal sokasodik.

Babai László Forrás: Wikimedia Commons/Bert Seghers

Fontos látni, hogy itt nem ügyes programozók algoritmusainak versengéséről van szó. Az, hogy egy probléma megoldása mennyire nehéz – illetve milyen ütemben nehezedik, ahogy a mérete nő –, a probléma matematikai szerkezetétől függ. Olyasmi, mint egy igen bonyolult csomó: a nehézsége a szerkezetében rejlik. Ha pedig ezt a szerkezetet megértjük, elképzelhető, hogy találunk benne ügyes trükkel magától kibogozódó részeket, másutt viszont marad az unalmas és ismétlődő ki- és befűzések sorozata.

Babai László Amerikában élő magyar matematikus másfél éve váratlan bizonyítást adott arra, hogy a gráfizomorfizmus-problémának létezik olyan megoldása, mely nagyon közel hozza az „egyszerűen kezelhető” (pontos szaknyelvi kifejezéssel: kvázipolinomiális) problémák családjához.

Pyber László első témavezetője Babai volt, majd Lovász László vette szakmai pártfogásába. Gráfelmélettel foglalkozott, így került kapcsolatba Erdős Pállal is, akinek a közös cikkek mellett néhány különös találkozót és több szombat hajnali telefonhívást is köszönhet.

Pyber azonban már a középiskolában – nevezetesen a Fazekas Mihály Gimnáziumban – beleszeretett a matematika egy másik területébe, a csoportelméletbe, és egy kilenc hónap alatt megszületett tételbizonyítás után úgy döntött, visszatér e kutatási irányhoz. A kombinatorikával töltött időszak azonban nem múlt el nyomtalanul: a csoportelméleti problémákat kicsit ilyen „szemüvegen” át is képes látni.

A Rubik-kocka forgatásai is csoportot alkotnak Forrás: Flickr/Steve Rhodes

II. A kapcsolatok fontosságáról

Mi az első matematikai művelet, ami az eszünkbe jut? Nyilván az összeadás – alaptulajdonságai annyira természetesek, hogy nem igazán foglalkozunk velük. Ha azonban egy kicsit hátralépünk, felismerhetjük, hogy az összeadás – és általában a matematikai műveletek – lényege, hogy kapcsolatot teremtenek dolgok között.

Két egész szám összege egy másik egész szám. Vegyük észre, hogy ez mennyire nem magától értetődő: az adószámok is egész számok, mégsem jut eszünkbe összeadni őket.

Ráadásul épp e kapcsolatteremtő tulajdonság miatt nem értelmezhetünk akármilyen műveletet akármilyen halmazon. A közismert összeadás működik mondjuk a páros számok halmazán, de a páratlanokén nem, hiszen két páratlan szám összege páros, vagyis az összeadás kivezet a halmazból.

Természetes gondolat tehát azt vizsgálni, hogy ha egy művelet – az összeadáshoz hasonlóan – kapcsolatot teremt egy halmaz elemei között, abból milyen szabályszerűségek következnek a halmazra és a művelet működésére.

Ha a művelet kielégít néhány nagyon egyszerű szabályt, az alapjául szolgáló halmazzal együtt csoportot alkotnak. Így csoportnak tekinthető az egész számok halmaza az összeadással, hasonlóan csoport a páros számok halmaza az összeadással, de csoportot alkotnak például egy szabályos ötszög szimmetriatranszformációi is – az ötszöget önmagába vivő forgatások, tükrözések –, ahol két transzformációt úgy „adunk össze”, hogy egymás után végezzük el őket.

Ez utóbbi példából látható, hogy vannak a csoportok között véges elemszámúak is, és nem meglepő módon a műveleti szabályok ezek szerkezetére is komoly hatással vannak. Az 1980-as évek közepére kiderült, hogy a véges csoportok építőköveinek tekinthető, ún. véges egyszerű csoportok osztályozhatók. Van néhány, bizonyos szabály szerint felépíthető sorozat és 26 darab kivétel. Gondoljuk csak végig: a matematikusok egy nagyon egyszerű, természetes módon kijelölt úton indultak el, és találtak 26 darab valamit. Ezek közül is kiemelkedik egy rejtélyes óriás, a Monster (magyarul: szörnyeteg), melynek egyre-másra fedezik fel kapcsolatait a matematika, sőt, az elméleti fizika legkülönbözőbb területeivel.

A véges egyszerű csoportok osztályozásának bizonyítása azonban nem olyasmi, amit az egyszeri matematikus csak úgy átfut. Tízezer oldalnál is terjedelmesebb, különböző hivatkozási helyeken fellelhető anyagról van szó, melynek ellenőrzése úgy tíz éve fejeződött be, egyszerűsítésén, tisztázásán pedig azóta is folyamatosan dolgoznak.

Ennek az osztályozásnak egy következményére épít egy helyen Babai gráfizomorfizmus-bizonyítása. Pyber Lászlónak pedig ezt a részt sikerült egy jóval egyszerűbb, e csoportelméleti „nagyágyút” nem használó ötlettel helyettesíteni úgy, hogy Babai tétele lényegében igaz maradt.

A matematikát sokan valamiféle elvont, önmagáért való tudománynak tartják, mások hatékony eszközök forrását látják benne, ha azonban valaki veszi a fáradságot, hogy elbeszélgessen egy valódi, hús-vér kutató matematikussal, komoly meglepetések érhetik. Gondolatokról, intuitív képekről fog hallani, dolgokról, „amelyek ott vannak”, „természetes” matematikai fogalmakról, „érdekes” tulajdonságokról vagy éppen „szép” bizonyításokról.

Az intuíció általában is fontos szerepet tölt be a tudományos munkában, de ha lehet, a matematikában mindennél fontosabb. Gyakran előfordul, hogy egy matematikus ráismer egy máshol már leírt struktúrára. Például egy halmazról és egy műveletről felismeri, hogy megfelelnek a csoporttól elvárt követelményeknek – és innentől a csoportelmélet teljes eszköztárát bevetheti a vizsgálatai során. De az sem ritka, hogy egy terület hosszas kutatása után – anélkül, hogy konkrét, nevesíthető struktúrákra mutatna rá – megsejt bizonyos tulajdonságokat, és sokszor érzi, milyen irányba érdemes elindulni.

Forrás: stockfresh.com

III. A sokféleség erejéről

Pyber egyszerűsítő ötlete egy izgalmas felismerésből ered, mely „szorzattétel” néven vált ismertté, és hamar kiderült, hogy csoportok bizonyos típusának egy olyan matematikai tulajdonságára tapintott rá, mely fontos eszközzé válhat mások kutatásaiban. Ahhoz, hogy a technikai részletek nélkül megértsük a lényegét, képzeljük el, hogy egy szakács szeretné az alapokról felépítve megérteni a thai konyhát.

Első lépésben készít egy listát az alapízekről, melyekből minden étel összetett ízvilága kikeverhető. Utána párosítani kezdi az ízeket, majd hármasával, négyesével keveri össze őket – és így tovább. Az összekevert ízek persze nem mind adnak különböző eredményt, előfordul, hogy két teljesen különböző keverék ugyanazt az összhatást adja, vagy egyszerűen értékelhetetlen.

A rengeteg kóstolgatás közben különös felfedezésre jut: három alapíz összekeverésénél ugrik meg igazán a kapott, gasztronómiailag értékelhető kombinációk száma. Kettő még nem elég, négy meg már nem ad annyit hozzá a dologhoz.

Később egy másik szakács rájön, hogy ez a „hármas” tulajdonság korántsem csak a thai konyha sajátja, hanem valahogy az ízeket és a főzést általában jellemzi, valami alapvetően fontos szabályszerűség, amely meghatározza, hogyan érdemes kevernünk az alapízeket, hogy sok új ízt kapjunk.

A valódi, matematikai történetben az „első szakács” egy Harald Helfgott nevű matematikus volt, aki a PSL(2, p) nevű egyszerű csoport generátorhalmazaira – tekintsük őket „alapízeknek”, melyekből a csoport műveletével kikeverhető az összes csoportelem – bizonyította ezt a furcsa „hármas” növekedési tulajdonságot. Két évvel később Pyber László és Szabó Endre – egyidejűleg Terence Taóval és két társával, de tőlük teljesen függetlenül – bebizonyította a tételt egyszerű csoportok egy jóval szélesebb körére.

Aki nagyon távolról figyeli a matematikát, annak úgy tűnhet, hogy nem egyéb sziklaszilárd állítások sokaságánál, és ebből a nézőpontból valóban jogosnak érezhetjük a matekórákon gyakran felmerülő kérdést: ha tudjuk, hogy igaz egy állítás, minek megtanulni a bizonyítást? Pedig a bizonyítás önmagában is izgalmas, rengeteget elmond a vizsgált matematikai objektumokról, segít jobban megérteni a tétel mögött álló kimondott vagy csak érezhető szabályszerűségeket, és sokszor egy-egy ötlet akár egy egész kutatási területet nyithat meg.

De akár eggyel hátrébb is léphetünk. A tételek és bizonyítások szigorú talaja felett kérdések izgalmas köde lebeg. Sokszor ezekben a kérdésekben ölt testet a matematikai intuíció, és az sem ritka dolog, hogy egy váratlan kérdés felvetése nagyobb elismerést vált ki a matematikusok közösségében, mint a rá adott bizonyítás.

Vannak viszont olyan gondolatok, kérdések, melyek – ahogy a való életben is – nehezen önthetők szavakba vagy írott formába, egy személyes beszélgetésben azonban mégiscsak átadhatók. Ilyen intenzív párbeszédben született meg például Pyber László egyik Erdős Pállal közös cikke, és ehhez hasonló beszélgetések zajlanak a matematikai konferenciák szüneteiben Los Angelestől Novoszibirszkig.

Az Oxford Internet Institute Twitter-kapcsolati hálózatának részlete Forrás: University of Oxford/Oxford Internet Institute - CC-BY-SA

IV. Az ezer szállal kötődésről

A szorzattétel önmagában is igen izgalmas eredmény, azonban a dolog nem állt meg itt, ugyanis egy Fields-érmes belga matematikus, Jean Bourgain és társszerzője, Alex Gamburd rájött arra, hogyan lehet a csoportok e váratlan növekedési tulajdonságának felhasználásával úgynevezett expandergráfokat konstruálni, melyek a matematika számos területén igen hasznosnak bizonyultak.

Ezzel visszajutottunk a hálózatokhoz. Az expandergráfok olyan hálózatok, amelyekben bárhogy választunk is ki kisebb részeket, azok mindig sok-sok szállal kapcsolódnak a külvilághoz.

Ha ránézünk a Facebook gigantikus kapcsolati hálózatára, intuitíve megérthetjük ezt a fogalmat. Nem igazán tudunk elképzelni olyan baráti kört, közösséget, amelynek nincsenek jócskán kifelé irányuló kapcsolatai. Ha azonban az emberiség ismeretségi hálózatait mondjuk 2-300 évvel ezelőtt ábrázoltuk volna, valószínűleg lettek volna olyan falvak, térségek, amelyek csak egy-egy szálon kapcsolódtak a külvilághoz. Tehát az a hálózat valószínűleg kevésbé volt „expanderjellegű”.

Az igazán „jó” expanderhálózatok pedig azok, ahol az egyes csúcspontok kevés kapcsolattal rendelkeznek, az egész hálózatnak mégis megvan az a tulajdonsága, hogy minden része sok szállal kötődik a többihez. Látszik, hogy ez a két feltétel ellentétes egymással: könnyű olyan hálózatokat készíteni, amelyekben a csúcsoknak kevés szomszédjuk van, és részeik gyakran „magukba fordulók”, és olyanokat is, ahol rengeteg a kapcsolódás és a csúcsoknak is sok szomszédjuk van.

A két ellentétes feltétel találkozásánál pedig, úgy fest, izgalmas, de bonyolult hálózatstruktúrák vannak – ezek felfedezésében segíthet az az új matematika, amelyet Pyber László és csapata az ERC Advanced Grant támogatásával tárhat fel. Az eddigi vizsgálatok egy váratlan mellékterméke volt Babai bizonyításának korábban említett egyszerűsítése.

Ráadásul Babai bizonyítása néhány további, a csoportelmélethez kapcsolódó elemet is tartalmaz, és Pyber csapatával a most elnyert támogatás keretében azt is megvizsgálja, esetleg lehet-e ezeken a pontokon erősíteni a tétel állításán. Még az is elképzelhető, hogy itt rejlik az a része a „csomónak”, melynek kibogozásával a gráfizomorfizmus-probléma átkerülhetne az „egyszerűen kezelhető” problémák családjába, vagyis P-be.

Pyber László negyedszerre rugaszkodott neki az ERC Advanced Grant pályázatának. Kicsit mindig ilyen szemmel is nézte a kutatásait, azonban be kellett látnia, hogy az ERC-pályázás szinte maga is egy tudományág, és ha valaki nem a pályázatírással kel és fekszik, az egész olyan, „mintha úgy tanulna az ember autót vezetni, hogy kétévente indul a Forma–1-en”. Első és második alkalommal kiesett az első körben, harmadjára bejutott a második fordulóba. Ez az eredmény tette lehetővé, hogy elnyerje az NKFIH 150 ezer eurós támogatását, majd végül 2016-ban sikerült, ami csak keveseknek: meglett az ERC Advanced Grant.

Most pedig utazik és csapatot épít, a támogatás pedig lehetővé teszi számára, hogy nagyobb kötöttségek nélkül válogasson a rendkívüli koponyák között. Csapatának oszlopos tagja lesz az a Szabó Endre, akivel egyebek mellett közösen jegyzik a nevezetes szorzattételt.

A két matematikus között semmiképp sem nevezhető hétköznapinak az együttműködés. Pyber egyszer épp akkor hívta fel Szabót egy matematikai kérdéssel, amikor kollégája a maratoni távot gyűrte egy versenyen. Előfordulnak ilyen bakik, mondhatnánk… Szabó azonban pár perc múlva visszahívta a válasszal!

„Van egy ír srác, aki valamiért szereti a régi csoportelméleti kérdéseimet” – ő valószínűleg része lesz a csapatnak, de Pybernek minden bizonnyal sikerül megnyernie tehetséges matematikusokat a világ más részeiről is. Konferenciákat rendeznek majd a témában, és könnyen megeshet, hogy a Rényi Intézet (ismét) a matematika egyik ígéretes, új ágának nemzetközi csomópontjává válik.